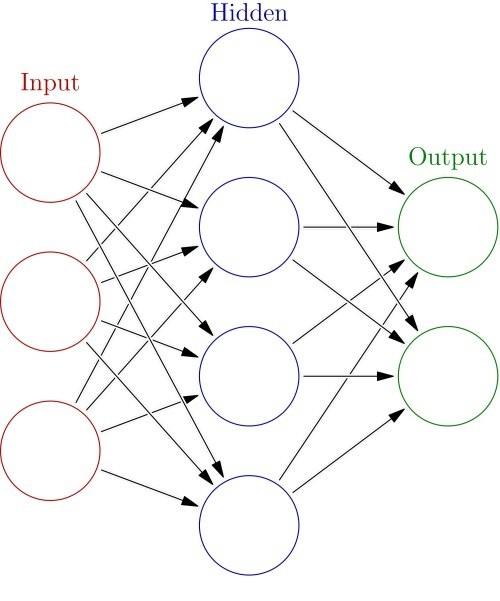
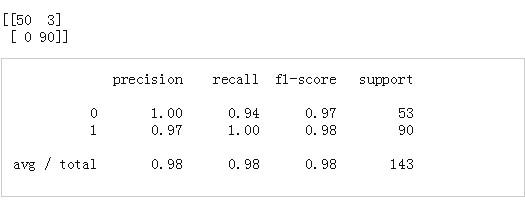
For Python, the most popular machine learning library is SciKit Learn. The latest version (0.18) was released just a few days ago and now has a built-in support for the neural network model. A basic understanding of Python is necessary to understand this article, and some experience with Sci-Kit Learn is also very helpful (but not necessary). Also, as a quick note, I wrote a detailed version of the sister article, but in R (can be viewed here). Neural networks are a machine learning framework that attempts to mimic the learning patterns of natural biological neural networks. A biological neural network has interconnected neurons with dendrites that accept input signals, and based on these inputs, they produce an output signal through the axons to another neuron. We will try to simulate this process by using an artificial neural network (ANN), which we now call a neural network. The process of creating a neural network begins with the most basic form of a single perceptron. Let's start our discussion by exploring the perceptron. The perceptron has one or more inputs, offsets, activation functions, and a single output. The perceptron receives the inputs, multiplies them by some weights, and passes them to the activation function to produce the output. There are many activation functions to choose from, such as logic functions, trigonometric functions, step functions, and so on. We also ensure that deviations are added to the perceptron, which avoids the problem that all inputs may equal zero (meaning that no multiplier weighting will have an effect). Check the visualization of the chart perceptron below: Once we have the output, we can compare it to the known tag and adjust the weight accordingly (the weight usually starts with a random initialization value). We continue to repeat this process until we reach the maximum number of allowed iterations or acceptable error rates. To create a neural network, a multilayer perceptron model of the neural network can be created starting from the overlay perceptron layer. An input layer that directly receives the input of the feature will be generated, and an output layer that will produce the resulting output. Any layer in between is called a hidden layer because they do not directly "view" the feature input or output. For visualization you can view the chart below (Source: Wikipedia). Let's start the practice and create a neural network with python! In order to keep up with the rhythm of this tutorial, you need to install the latest version of SciKit Learn. Although it is easy to install via pip or conda, you can refer to the official installation documentation for complete details. We will use SciKit Learn's built-in breast cancer dataset, if samples with tumor characteristics are labeled and show whether the tumor is malignant or benign. We will try to create a neural network model that understands the characteristics of the tumor and tries to predict it. Let's move on, start with getting the data! This object is like a dictionary, containing the description information, characteristics and goals of the data: Let's divide the data into training and test sets and test the split function from the training of SciKit Learn's in the pattern selection, which is easy to do. | Data preprocessing If the data is not normalized, the neural network may be difficult to aggregate until the maximum number of iterations is granted. Multilayer perceptrons are very sensitive to feature scaling, so it is highly recommended that you scale the data. Note that the same scaling must be applied to the test set to get meaningful results. There are many different methods of data standardization that we will standardize with the built-in StandardScaler. It is time to train our model. By estimating objects, SciKit Learn makes it extremely easy. In this case, we will import our estimator (multilayer perceptron classifier model) from SciKit-Learn's neural_network library. We will next create an instance of the model, you can define a lot of parameters and customization, we will only define hidden_layer_sizes. For this parameter, you pass a tuple containing the number of neurons you want at each level, where the nth entry in the tuple represents the number of neurons in the nth layer of the MLP model. There are many ways to choose these numbers, but for the sake of simplicity, we will choose the same number of neurons as the three layers of our dataset: Now that the model has been built, we can put the training data into it and remember that it has been processed and scaled: MLPClassifier(acTIvaTIon='relu', alpha=0.0001, batch_size='auto', beta_1=0.9, Beta_2=0.999, early_stopping=False, epsilon=1e-08, Hidden_layer_sizes=(30, 30, 30), learning_rate='constant', Learning_rate_init=0.001, max_iter=200, momentum=0.9, Nesterovs_momentum=True, power_t=0.5, random_state=None, Shuffle=True, solver='adam', tol=0.0001, validaTIon_fracTIon=0.1, Verbose=False, warm_start=False) We can see the default output of other parameters in the display model. Try to use multiple values ​​with different values ​​to see the impact of the data on the model. Now that we have a model, it's time to use it to get predictions! We can simply use the predict() method in our fitted model: Now we can use SciKit-Learn built-in metrics such as classification reports and confusion matrices to evaluate how our model performs: It seems that only three cases have been misclassified, with an accuracy rate of 98% (and 98% accuracy and recall). Considering that we wrote so little code, the effect is quite good. However, the disadvantage of using a multi-layer perceptron model is that there are many difficulties in interpreting the model itself, and the weights and deviations of the features are difficult to interpret easily. However, if you want to extract MLP weights and biases after training the model, you need to use its public properties coefs_ and intercepts_. Coefs_ is a list of weight matrices, where the weight matrix at index i represents the weight between layer i and layer i + 1. Intercepts_ is a list of deviation vectors, where the vector at index i represents the offset value added to layer i + 1. I hope you enjoy this short discussion about neural networks. We can try to play with the number of hidden layers and neurons and see how they affect the results. Product description: 5L Air Fryer,Air Fryer Deep,Hot Air Fryer,Industrial Deep Fryer Ningbo Huayou Intelligent Technology Co. LTD , https://www.homeapplianceshuayou.com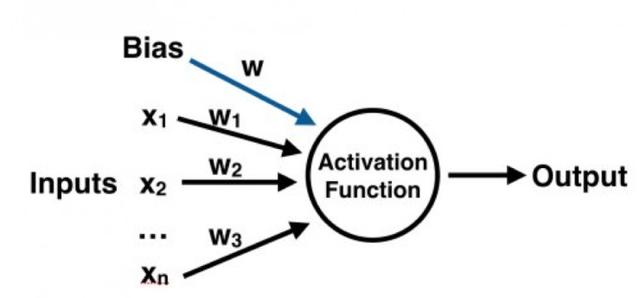

Removable frying pot&basket with non-stick coating
Automatic shut-off with ready alert
304 stainless steel heating element
Heat resistant material inside enclosure
Removable and heat insulation handle for frying basket
Prevent slip feet
With fan guard,more safety
Certificates: GS CE CB SAA RoHS LFGB
Colour: customized
English manual&cookbook